深浅模式
数量规律
字数: 0 字 时长: 0 分钟
考查频次:数量规律是图形推理中考查最多、变化最多的考点。它可以单一考点命题,也可以两个考点结合命题(如面和线结合的考法),还可以和其他规律结合命题(如数量规律和属性规律的复合考法)
题型特征:图形元素组成不同
解题思路:当图形元素组成不同时,常考查属性、数量及其他特殊规律。当题干图形无明显属性规律时,可优先考虑数量规律。常考的数量规律有五种:点、线(笔画)、面、素、角。图形元素组成不同,且无明显属性规律。
一、点数量
1、在图形推理中,,下面五幅图中标灰的点就是交点。
2、,即由相切关系得到的交点,如图5,共有 3个交点,其中有2个点为切点。(
注意:切点是交点,交点不一定是切点)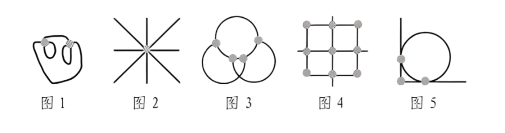
3、当有以下特征图时,可能考察点的数量规律
- (1)线条交叉明显(比如米字形)
- (2)绕来绕去的一团线
- (3)切点(或顶点)较多
4、注意考察点的形式:
5、数点情况:
- (1):
- ①交点的数量成等差数列
- ②交点的数量无序,但是可以排成有序。比如题干给四幅图,前四幅图的交点数量分别为3、1、5、2;即答案选择4个交点的,排成有序。
- (2):内部和外部交点;内部线条与外框的交点。
- (1):
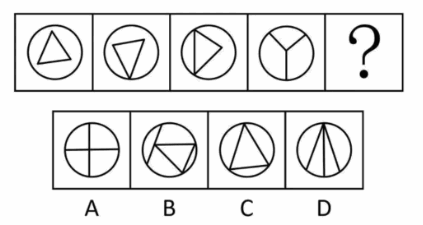
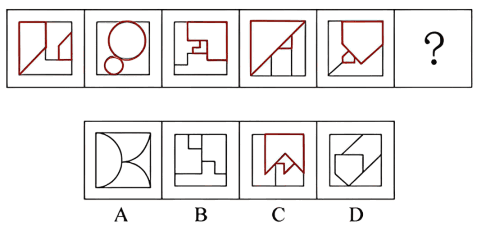
(2023广东)从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性。
解析
- 观察发现,题干图形均由圆形外框和内部直线构成,且内部直线与外框有明显交叉,考虑框上交点数,题干图形的框上交点数依次为0、1、2、3,故?处应选择框上交点数为4的图形,排除C项;
- 继续观察发现,题干前三幅图形中均出现三角形,考虑直线数,题干图形的直线数均为3,故?处应选择直线数为3的图形,只有D项符合。
- 故正确答案为D。
二、线数量
1、当有以下特征图时,可能考察线的数量规律:
- (1)如果图形出现的,可以优先考虑数的数量;
- (2)如果图形出现的,可以优先考虑数的数量;
- (3)如果图形出现半曲半直图形,注意考察;
2、注意:
(1)。
(2)3+2类型题目,可能会考察线的数量求和为定值。
(3)九宫格可能会考察:①线的数量求和为定值;②每行或每列线的数量求和呈等差。
(4)
(5):①考察平行线的;②平行线的方向。
(2019江苏)从四个图中选出唯一的一项,填入问号处,使其呈现一定的规律性
解析
- 首先观察题干所有图形,发现都有一个圆形外框,所以问号处也应该是圆形外框,排除BC;
- 进一步观察题干,发现图2圆内部就是一条单一的直线,图3的圆内部也有单一直线,图4和图5,图形内部都是多边形,所以优先考虑数直线数量,图1到图5,圆形内部的直线数量分别为01234,所以问号处应该是圆形框内部有5条直线的图形,排除A,选D。
- 正确答案为D。
(2014深圳)从所给四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性:
解析
- 思路一:
- 观察发现,题干每幅图均由一个小黑圆和若干直线组成,虽然小黑点的位置在发生移动,但并没有规律。
- 因此观察直线,发现,第一组图直线数分别为3,2,3,相加之和为定值8,第二组前两幅图直线数分别为2,4,因此?处应选择一个直线数为2的图形,只有D项符合。
- 思路二:
- 观察发现,题干每幅图均由一个小黑圆和若干直线组成,虽然小黑点的位置在发生移动,但并没有规律。
- 再次观察发现,题干出现线线相交,因此考虑数交点。第一组图交点数分别为2,1,2,相加之和等于5,第二组图前两幅图交点数分别为1,3,因此?处应选择一个交点数为1的图形,只有D项符合。
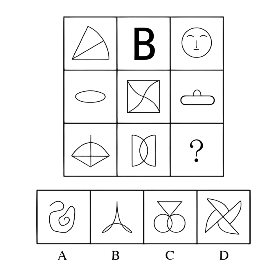
(2017国家)从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性。
解析
- 观察发现,曲线特征明显,考虑数曲线。
- 九宫格,横向规律较为常见,优先考虑。
- 第一行中曲线数依次为1、2、3,呈等差规律;
- 第二行验证,符合规律;第三行应用规律,前两幅图曲线数依次为1、2,只有B项符合。
- 因此,选择B选项。
三、面
1、面数量
(1)面:指注意黑色不是面。
(2)数面的特征图:①图形被分割;②封闭区域明显;③生活化图形。
(3)注意:如果同时出现数面、数线、数笔画、数点的特征图,优先数面
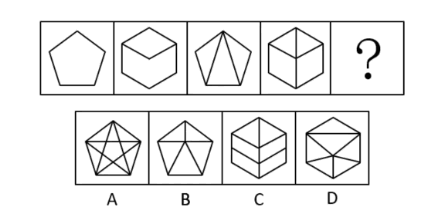
(2019广东)从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性。
解析
- 观察发现,图2到图4图形均被分割为多个封闭空间,考虑面数量。
- 题干图形的面数量分别为:1、2、3、4、?,则?处应为5个面的图形。
- A项11个面,排除;B项5个面,当选;C项6个面,排除;D项6个面,排除。
- 故正确答案为B。
2、特殊面
- (1):
①。下面图1的面都是三角形,图2的面都是四边形。
②。特别明显的大面或小面,我们可以将其勾画出来进行对比。如下面图3的最大面是三角形,图4的最大面是四边形。考点:。
(2019北京)从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性。
解析
- 第一组图形中面的数量均为4,第二组前两幅图形中面的数量均为5,但选项中面的数量也都为5,所以看面的数量无法得出正确答案。
- 需要我们再进一步观察,第一组图形中的面都是三角形,第二组前两幅图形中的面都是四边形,所以?处也应该选择一个所有面都是四边形的图形。所以答案选D
(2022国家)从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性。
解析
- 图形面的数量依次为4、4、4、5、4,面的数量不存在规律,可进一步观察面的大小,发现图形中存在明显的最大面和最小面,且最大面和最小面的形状相似,A、B项中两个相似的面大小均相同,D中不存在两个相似的面。
- 答案选C。
(2):每幅图都存在一部分全黑或者阴影的面。
①结合九宫格:通过所占格子面积、个数成规律。
②对称性:整体看图形没什么规律,黑色面和白色面各自都存在对称性,需要结合对称性的考点进行分析。
③其他图形关系:如相同黑面和相同白面的关系,黑面与外框形状关系。
(2019山东选调)把下面的六个图形分为两类,使每一类图形都有各自的共同特征或规律,分类正确的一项是:
解析
- 题每个图形整体上来看虽然都不对称,但是每幅图中的三个小图形均为对称图形,因此,可以分别画出每幅图形中三个小图形的对称轴,发现图①③④黑块的对称轴和一个空白图形对称轴平行,和另一个空白图形对称轴交叉;图②⑤⑥黑块的对称轴和两个空白图形的对称轴都交叉,因此,①③④一组,②⑤⑥一组。
- 故正确答案为A。
(2025国家)把下面的六个图形分为两类,使每一类图形都有各自的共同特征或规律,分类正确的一项是:
解析
- 题干每幅图形均由多个面和一个黑块拼接而成,考虑图形间关系。观察发现,图①②⑥中黑块与图形外框均有1条公共边,图③④⑤中黑块与图形外框均有0条公共边,即图①②⑥为一组,图③④⑤为一组。
- 故正确答案为A。
(2019上海)下列选项中,符合所给图形的变化规律的是______。
解析
- 每幅图形均为九宫格,且存在黑色区域。观察发现,第一组图中,每幅图形中的黑色区域均占3个格子;第二组图中,前两幅图黑色区域均占6个格子,故?处图形黑色区域应占6个格子,只有C项符合。
- 故正确答案为C。
3、面的数量复合
(1)可能考察面数量和外框边数(是否相等、求和、求差)。
(2)面数量和交点数。
(3)存在相同面。考察相同面个数、组数。
(2017广州)请选择最适合的一项填入问号处,使之符合之前四个图形的变化规律。
解析
- 元素组成不同,且无明显属性规律,优先考虑数量规律。
- 图形特征较为明显,窟窿比较多,因此考虑数面,题干图形面数量依次为1、4、2、2、?,无规律,图形均为直线组成,数直线,题干图形直线数量依次为3、8、5、5、?,无规律。
- 再观察发现,题干图形外框的直线数为3、6、4、4、?,观察数字发现,每个图形外框直线数与该图形面数量之差均为2。
- 因此?处也应选择一个外边框线条数量和面数量差为2的选项,只有B项符合。
四、角
角由两条具有共同端点(顶点)的射线构成,射线是直的。所以角的边不可以是曲线。
1、角数量
(1)。角还可以细分为。一般直角考的多。
(2)
(3)
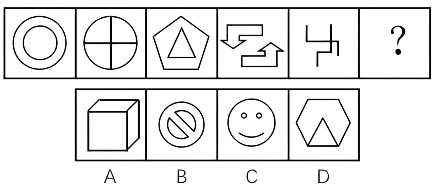
(2015浙江)从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性。
解析
- 观察发现,图 4 与其他图形明显不同,从该图特征入手。
- 该图由两条互相垂直的直线组成,则相关的数量类规律只有点、线和角。再观察发现题干和选项中多次出现直角,所以优先考虑直角的数量规律。
- 题干给出的四个图形中直角的个数分别为 1、2、3、4,则问号处图形的直角个数应该是5,只有 D 项符合。故正确答案为 D。
2、角的特殊考法
(1)外框直角数:内部凌乱或有图形没内部,则看外框,考虑外框的线条、外框的角数
(2)直角复合旋转:直角数量复合角度旋转。
(3)角与元素标记复合:元素标记的角(锐角、直角、钝角)。
(4)相同角。
(2023浙江C)从所给的四个选项中选择最合适的一个填入问号处,使之呈现一定的规律性:
解析
- 图形元素组成不同,且无明显属性规律,考虑数量规律。
- 观察发现,题干每幅图都是由直线构成,存在直线相交且出现明显的直角,优先考虑数直角数。
- 图形大多分为内、外两部分,考虑分开数直角数。
- 外框图形直角数依次为0、1、2、3、4、“?”,所以“?”处应该选择一个外框直角数为5的图形,只有B项符合。
(2023北京)请从四个选项中选出最恰当的一项填在问号处。
解析
- 元素组成不同,且无明显属性规律,优先考虑数量规律。
- 观察发现,每幅图均由直线构成,且每幅图中均由横线和竖线构成一个直角,且直角位置顺时针旋转,分别位于右下、左下、左上、右上、右下,故?处直角位置应在左下,故正确答案为A。
(2015广东乡镇)从所给的四个选项中,选择最合适的一项填在问号处,使之呈现一定的规律性:
解析
- 出现小黑点,考虑功能元素,考虑点与其他元素之间的位置关系,发现所有黑点都仅出现在图形的锐角处,A、B 两项存在直角处小黑点,C 项存在钝角处小黑点,排除 A、B、C 三项。
(2018广州40%)请选择最适合的一项填入问号处,使之符合整个图形的变化规律。
解析
- 图形元素组成不同,无明显属性规律,考虑数量规律。第一行中,图一有两个相同的锐角,图二有两个相同的直角,图三有两个相同的钝角;第二行经验证规律一致,所以第三行也应符合此规律,即图一有两个相同的锐角,图二有两个相同的直角,故?处应有两个相同的钝角,但发现此时无正确答案。观察发现,题干中每幅图都有两个相同的角,此时只有A项有两个相同的直角,B、C、D三项均无两个相同的角,因此选择A项。本题只需要考虑每幅图均有两个相同的角,不需要考虑角的大小。
- 故正确答案为A。
五、元素(部分)数量
1、元素,可细分为3种情况。
2、图1,元素的个数是5,元素种类数是3(正方形、五角星、圆),部分数是5;
3、图2,元素的个数是5,元素种类数是4(正方形、五角星、圆、桃心),部分数是5
4、图3,元素的个数是3,元素种类数是3(五角星、四角星、椭圆),因为这三种小元素都连在了一起,因此部分数是1

5、当图形由很多,可以数元素的个数、种类;
6、题目特点:
- (1)元素凌乱
- (2)多个小图形或多个线条
- (3)加粗黑体
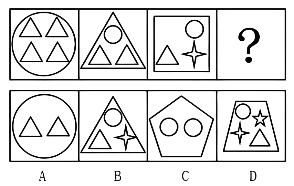
(2015湖北选调)从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性。
解析
- 图形元素组成不同,且无明显属性规律,考虑数量规律。
- 观察题干图形内部小元素种类,依次为1、2、3、?,则?处应为内部有4种小元素的图形,只有D项符合。故正确答案为D。
六、笔画
1、考点:大部分考
2、笔画数的特征图:,优先考虑笔画数。
3、判断图形的笔画:对于简单图形,可通过临摹的方式直接得出,而对于复杂图形,可通过下列公式进行计算:连通图的(
奇点是以某个点为起点,延伸出的线条数为奇数)。其中。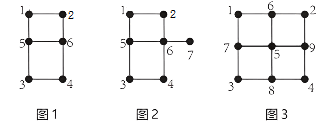
(1),以点 1、2、3、4 为起点,延伸出来的线都是 2 条,偶数条,因此它们均为偶点;以点 5、6 为起点,延伸出来的线都是 3 条,奇数条,因此它们均为奇点。图 1 奇点数为 2,可以一笔画完成
(2),以点 1、2、3、4 为起点,延伸出来的线都是 2 条,偶数条,因此它们均为偶点;以点 6 为起点,延伸出来的线为 4 条,偶点;以点 5 为起点,延伸出来的线为 3 条,奇点;以点 7 为起点,延伸出来的线为 1 条,奇点。图 2 奇点数为 2,可以一笔画完成。
(3),以点 1、2、3、4 为起点,延伸出来的线都是 2 条,偶点;以点 5 为起点,延伸出来的线为 4 条,偶点;以点 6、7、8、9 为起点,延伸出来的线为 3 条,奇点。图 3 奇点数为 4 个,笔画数 =4÷2=2,故须两笔画才能完成
6、简化一笔画判断之吹捏法:在图形复杂性增加时,数奇点也会变得繁琐且耗时。而吹捏法完全摒弃了这一步骤,只需通过简单的铅笔画,即可迅速得出答案。
(1)吹捏法步骤:先识别并“捏掉”图形中的的外轮廓线条,直到没有封闭面。注意原图是多部分分离图形要分开捏,最后分别加上捏后的笔画,如下图最后三角形和圆。
(2)分析剩余结构:对剩余结构数笔画即可。(
如果最“捏”没了,即剩余部分为空,则为1笔画)
(2018国家)把下面的六个图形分为两类,使每一类图形都有各自的共同特征或规律,分类正确的一项是:
- A. ①②⑥,③④⑤
- B. ①②⑤,③④⑥
- C. ①②③,④⑤⑥
- D. ①③⑤,②④⑥
解析
- 本题为分组分类题目。图形元素组成不同,无明显属性规律,考虑数量规律。
- 观察发现,图①为“日”字的变形图,图⑤为多圆相交,考虑笔画数。
- 图①②⑤的奇点数都是2,为一笔画图形,图③④⑥的奇点数都是4,为两笔画图形。
- 即图①②⑤一组,图③④⑥一组。
- 故正确答案为B。
七、随笔练习
例1:(2009四川)从所给四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性:
解析
- 观察图形交点明显,都是的。
- 第一组图形中,两图交点数量都为2;第二组图形,两图交点数量交点数量为3,那么第三个图形的交点数量也应为3,只有C符合。
例2:(2019 联考)从所给的四个选项中,选择最合适的一个填入问号处, 使之呈现一定的规律性:
解析
- 题干图形。
- 题干面数量依次为 2、3、4、5、6、?,故“?”处应该选择面数量为 7 的图形,对应 C 项。
例3:(2017河南)从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性。
解析
- 图形。
- 面数量分别为3、4、5、6、7、?,问号处需填8个面的图形,选项面数量分别为9、8、8、8,排除A项。考虑面考点细化发现,每个图形被分割最大面均为三角形,故答案为B。
例4:(2014浙江)请从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性:
解析
- 题干中出现。
- 观察已知的图形,角的个数分别为3、5、7、9,形成等差数列,因此问号处的图形应该有11个角,只有C项符合。故正确答案为C。
例5:(2016广西)把下面的六个图形分为两类,使每一类图形都有各自的共同特征和规律,分类正确的一项是:
- A. ①②⑥,③④⑤
- B. ①③④,②⑤⑥
- C. ①⑤⑥,②③④
- D. ①③⑤,②④⑥
解析
- 图形元素组成不同,优先考虑属性规律,但无唯一答案。
- 观察发现,题干图形出现了粗线条和生活化图形,考虑部分数。
- 图①③⑤的部分数均为1,图②④⑥的部分数均为2。故图①③⑤为一组,图②④⑥为一组。
- 故正确答案为D。
例6:(2018江苏)从四个图中选出唯一的一项,填入问号处,使其呈现一定的规律性。
解析
- 图形元素组成不同,无明显属性规律,考虑数量规律。
- 观察发现,。
- 题干均为两笔画图形,A项为两笔画图形,B项为三笔画图形,C项为四笔画图形,D项为一笔画图形,只有A项满足。
例7:(2020浙江)从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性:
解析
- 第一段中,所有图形中均有 2 组平行线;第二段中,前两个图形中均存在 3 组平行线,所以问号处的图形中也应存在 3 组平行线,只有 A 项符合。
例8:(2019国家)把下面的六个图形分为两类,使每一类图形都有各自的共同特征或规律,分类正确的一项是:
- A.①③④,②⑤⑥
- B.①②⑥,③④⑤
- C.①③⑤,②④⑥
- D.①④⑥,②③⑤
解析
- 本题为分组分类题目。观察图形发现,多边形内部被线条分割,优先考虑数面的数量,但题干图形的面数量都是5,无法分组。继续观察发现,图①③⑤中存在明显最小的面,且最小的面的形状均与图形外轮廓形状相同,图②④⑥中存在明显最大的面,且最大的面的形状均与图形外轮廓形状相同,故①③⑤一组,②④⑥一组。 故正确答案为C。
例9:(2019河南司法)从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性:
解析
- 元素组成不同,且无明显属性规律,考虑数量规律。
- 题干图形出现明显的多边形以及单一曲线,考虑数线条数。九宫格优先横着观察,三行图形依次由1,2,3,4,5,6,7,8,“?”条线组成。故“?”处应该选择由9条线组成的图形,对应B选项。
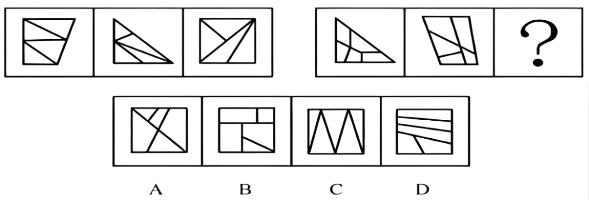
例10:(2018江苏)从四个图中选出唯一的一项,填入问号处,使其呈现出一定的规律性。
解析
- 元素组成不相同且属性无明显规律,考虑数量规律。
- 观察图形发现,题干展开图中出现多边形和单一直线,考虑数直线数。整体数直线无规律,考虑内外分开数。
- 每幅图外部直线数分别为:6、5、4、4、5,内部直线数分别为:5、4、3、3、4,发现每幅图外部直线数-内部直线数=1,故?处也应该选择一个符合此规律的图形,只有A选项符合。
例11:(2024江苏34%)请从四个选项中选出最恰当的一项填入问号处,使题干图形呈现一定的规律性。
解析
- 元素组成不同,优先考虑属性规律。观察发现,题干出现全直线、全曲线图形,可以考虑曲直性。九宫格优先看横行,第一行图形分别为有曲有直图形、全曲线图形、全直线图形;经验证,第二行符合此规律;第三行应用此规律,故“?”处图形应是全直线图形,排除B项;
- 继续观察发现,题干图形出现明显封闭空间,考虑面数量,第一行图形面数量均为1,第二行图形面数量均为2,第三行前两幅图形面数量均为3,故“?”处图形面数量应为3,排除C项;
- 对比A、D两项,A项图形部分数为2,D项图形部分数为1,题干图形部分数均为1,只有D项符合。
- 故正确答案为D。
例12:(2023广东事业单位)请从所给的四个选项中,选择最合适的一个填入问号处,使之呈现一定的规律性( )。
解析
- 元素组成不同,且无明显属性、位置规律,优先考虑数量规律。观察发现,题干图形中黑块全部相连,考虑笔画数。题干中所有由黑块构成的图案都能由一笔画成,故?处应选择黑块构成的图案能够被一笔画成的选项,只有C项符合。
- 故正确答案为C。