图形数列

   而图形题相较于分数数列、递推数列、多级数列等常见纯数字数列来说，在没有掌握一些常见技巧的前提下确实无从下手。目前在江苏、浙江、广东、吉林等有可能考查到这一考点，还有部分事业单位的考试。

一、题型特征

   题干出现图形，常见的有圆圈题、三角形题、以及3×3或4×4方格形。圆圈题和方格形是图形题中最常考的题目。

圆圈

   圆圈题分为两种，一种是的题目，另一种是的题目。

（一）有圆心

   有圆心的题目难度相对简单一些，其大致样式如下图：

1. 解题技巧：

2. 举个栗子：

1. 分析：本题为圆圈题中带圆心的题目，首先考虑对角线的数字能否通过运算得到圆心的数字，第一个圆圈中发现15-8=7，21÷3=7，用此规律验证第二个圆圈：10-6=4,24÷6=4，规律正确。则最后一个圆圈问号处的数字为16-2=42÷3=14，故本题第4个中间值为14。

（二）无圆心

   无圆心的题目考查几率较大，其中2018年浙江省省考考查了4个此类题目。

1. 解题技巧：

2. 举个栗子：

1. 分析：在分析无圆心的圆圈题时，首先考虑对角线的两个数做差，其次是做和或相乘，如果有明显的倍数关系可考虑做商。本题首先考虑对角线的数做差，4-2=2,3-1=2，做差后相等。验证第二个圆圈，5-9=-4，4-（-1）=5，做差后不相等，规律出现错误。观察第一个圆圈发现，4是2的两倍，4÷2=2，3-1=2，一个做商一个做差，然后相等。以此验证圆圈二，4÷-1=-4，5-9=-4，满足此规律，验证圆圈三，10÷-5=-2,6-8=-2，满足规律，则括号内的数应该为2，故本题答案为2。

三角形

   三角形题目的样式一般如下图所示：

1. 解题技巧：

2. 举个栗子：

1. 分析：中间的数字明显大于周围的三个数字，优先考虑加法或者乘法。外围三个数直接相加并不能得到中间的数，因此考虑加法与乘法相结合。发现（2+3）×5=25，（4+8）×6=72，（3+7）×9=90，则问号处的数字为102÷（8+9）=6，故本题答案为6。

方格形

   一般考察3×3，3×4，4×4。九宫格考查的几率较大，此类题目看似难度较大，实则在掌握常见解题方向和技巧后难度并不大。

1. 解题技巧：

   1. （1）分行或列成等差或等比数列；
   2. （2）各行或列单独计算为常数
   3. （3）各行或列内部凑数字之间相等关系（+-×÷），比如每行数列中其中两项通过一定的预算得到第三项；

2. 举个栗子：

1. 分析：分行或分列看，数字之间没有明显的等差或等比，排除分行或分列成等比数列。接下来考虑分行或分列数字加和，发现每行数字之和为5，问号处应填入-5，故本题答案为-5。

三、总结

1. 以上是常见的图形数列，但在考试中可能会出现其他创新图形，比如六边形、奇怪的形状。因此根据常见的图形数列总结3个解题思路：
   1. （1）
   2. （2）
   3. （3）

四、随笔练习

1. 例1：（2019浙江）
2. 
3. A.10    B.12
4. C.14    D.16

：题目特征明显，为，观察其他数字与中心数字的关系，因为第二项、第三项中心数字均比周围数字大，故可以此为突破口找规律，考虑加法、乘法等可以使数字变大的方法。
第一个数阵中 5×2-5=5
第二个数阵中 3×3-3=6
第三个数阵中 2×7-4=10
即。则第四个数阵中，4×6-?=10，解得?=14。

1. 例2：(2014深圳)仔细观察数列的排列规律，然后从四个选项中选出最符合规律的一项来填补空缺项。
2. 
3. A.2    B.8
4. C.9    D.10

：题目特征明显，，观察其他数字与中心数字的关系。第一项中心数与已知项的其他中心数相比最小，为5，从最小的入手，找到规律之后用其余项来验证此规律是否成立。
观察第一项，可得4×3-(5+2)=5，即第一项规律为。用第二项验证:6×4一(2＋4)=18，此规律成立。故题干所求项应为3×6-(2＋7)=9。
故正确答案为C。

1. 例3：(2017广州)观察表中数字的变化规律，依次填入空格X、Y中的数字是:
2. 
3. A.5，81    B.5，121
4. C.7，81    D.7，121

：题目特征明显，为。凑大数，先观察图形，大数在每一列的最后一个且均为平方数，再找每一列其余数字与大数之间的关系即可求解本题。
第一、二、四列的大数分别为36、49、225，依次为6、7、15的平方。观察每一列，发现第一列和第四列的第三行数恰好为6、15，且前两行数字之和等于第三行数字：4＋2=6、6+5= 11、8＋7=15，故每一列规律为：第一行＋第二行=第三行、(第一行＋第二行)×第三行=第四行，则X=3＋4=7，Y=(6+5)×11=121。故正确答案为D。

1. 例4：(2020上海)如图，问号处的数字为:
2. 
3. A.1    B.8
4. C.19    D.31

：观察数列特征，没中心凑大数。第一个数阵中最大的数是右上角的19、第二个数阵中最大的数是左上角的23、第三个数阵中最大的数是左下角的27，。
先考虑加法，第一个数阵:1+19+10+4=34，第二个数阵:23+13+6+2=44，第三个数阵:16+8+3+27=54，构成数列：34、44、54，此数列是公差为10的等差数列，则其下一项为54+10=64。即第四个数阵:10+4+ ?+19-64，则?=31。

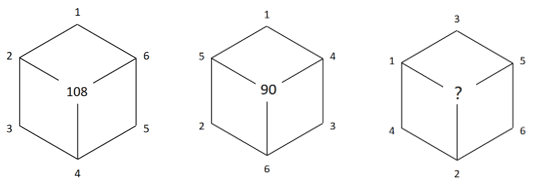
1. 例5：(2022上海37%)根据下列图形上的数字规律，“？”处的数字应为______。
2. 
3. A.64    B.88
4. C.96    D.104

：图形数列，有中心优先凑中心：
第一个图形：（2+4+6）×（1+3+5）=108；
第二个图形：（5+6+4）×（1+2+3）=90。
规律为在每个正六边形中，与中心数字相连的三个数之和×其他三个数之和=中心数字。
根据以上规律，第三个图形中，？=（1+2+5）×（3+4+6）=104。故正确答案为D。

1. 例6：(2018浙江)把最合适的一项填入？中，使其符合一定的规律：
2. 
3. A.-4    B.-2
4. C.0    D.2

：图形数阵，考虑对角线方向的数字联系。
第一个数阵中，3-1=4÷2；
第二个数阵中，5-9=4÷（-1）；
第三个数阵中，6-8=10÷（-5）
故第四个数阵中，3-2=？÷2，？=2。故正确答案为D。

1. 例7：(2020广东)把最合适的一项填入？中，使其符合一定的规律：
2. 
3. A.16    B.27
4. C.38    D.49

：图形数阵，优先考虑横向和竖向规律。各行或列单独计算为常数。
第一行 4+5+7=16；
第二行 8+8+16=32；
第三行 12+9+27=48；
发现各行数字之和组成的数列16，32，48，（ ），是公差为16的等差数列，下一项为48+16=64，则所求项=64-16-10=38。故正确答案为C。

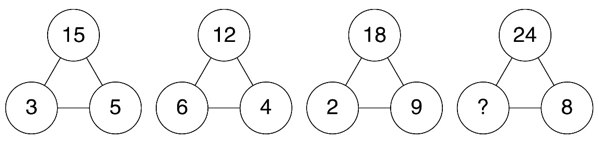
1. 例8：(2023上海)根据下列数字关系，“?”中的数字不可能是_____。
2. 
3. A.3    B.6
4. C.9    D.12

：观察题干发现，各数阵之间无法形成统一的递推规律，考虑数字特性。分析可得，3与5均为15的约数，6与4均为12的约数，2与9均为18的约数，即在每个数阵中，下面两个数字均为上面数字的约数。按此规律，选项中只有C项9不是24的约数，C项当选。