十字交叉

十字交叉法实际上是一种方程计算过程中的简化形式。，在行测中资料分析以及数量关系都会涉及到。

一、十字交叉法

1. 1、方法来源：十字交叉法最先是从溶液混合问题（）衍生而来的。公式：浓度（%）=$\frac{\mathrm{溶}\mathrm{质}}{\mathrm{溶}\mathrm{液}}$；若有两种溶液的质量分别为 $A$ 与$B$ ，其浓度分别为 $a$ 与 $b$，混合后浓度为 $r$，则由可列出下式 $Aa+Bb=(A+B)r$，对上式进行变形可得$\frac{a}{b}=\frac{r-b}{a-r}$，在解题过程中一般将此式转换成如下形式：
   

2. 2、注意：

3. 3、口诀：

二、适用题型

1. 1、该方法一般适用于平均值的混合问题的题型，比如说：混合溶液、利润率、折扣、增长率、比重、平均数等，公式如下。
2. 2、公式：：看到了符合以下的公式且存在的题目一般都能够运用十字交叉法。
   1. 浓度（%）=$\frac{\mathrm{溶}\mathrm{质}}{\mathrm{溶}\mathrm{液}}$
   2. 利润率（%）=$\frac{\mathrm{利}\mathrm{润}}{\mathrm{成}\mathrm{本}}$
   3. 折扣（%）=$\frac{\mathrm{售}\mathrm{价}}{\mathrm{原}\mathrm{价}}$
   4. 比重（%）=$\frac{\mathrm{部}\mathrm{分}}{\mathrm{整}\mathrm{体}}$
   5. 增长率（%）=$\frac{\mathrm{增}\mathrm{长}\mathrm{量}}{\mathrm{基}\mathrm{期}\mathrm{量}}$
   6. 平均数=$\frac{\mathrm{总}\mathrm{数}}{\mathrm{人}\mathrm{数}}$
   7. 比如：A班女生的比重为45%，B班女生的比重为60%，AB班女生的比重为55%。比重=女生/全班人数
   8. 利用口诀：A班人数/B班人数=5%/10%

三、线段法

线段法是十字交叉法的变形，只是换了一种画法而已

1. 若有两种溶液的质量分别为 $A$ 与$B$ ，其浓度分别为 $a$ 与 $b$，混合后浓度为 $r$，
2. 口诀：
   1. （1）部分写两边，整体写中间。
   2. （2）距离和量成反比。（距离是指混合后的的距离和两端做差）
   3. 上面的图根据口诀可得：$\frac{a}{b}=\frac{r-b}{a-r}$

四、随笔练习

例1：（2014四川）学校体育部采购一批足球和篮球，足球和篮球的定价分别为每个 80 元和 100 元。由 于购买数量较多，商店分别给予足球 25%、篮球 20% 的折扣，结果共少付了 22%。问购买的足球和篮球的数量之比是多少？（ ）

1. A.4：5
2. B.5：6
3. C.6：5
4. D.5：4

解析

6. 方法一：总折扣=折扣后总额/折扣前总额，足球部分少付了25%，篮球部分少付了20%，混合后少付了22%，典型 A，B 的混合题型，因此采用十字交叉法如下：
   
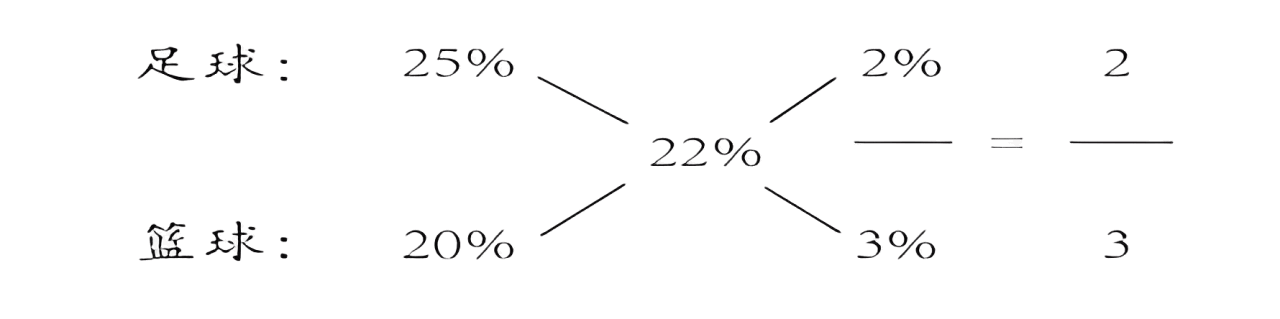
   即足球价格总额与篮球价格总额之比为 2：3。注意该比例是足球折扣前总额和篮球折扣前总额的比，设足球共买了 x 个，篮球共买了 y 个，则可列式为 80x：100y=2：3，解得 x：y=5：6。故本题选 B
7. 方法二：设足球共买了 a 个，篮球共买了 b 个，根据混合列式有25%×80a+20%×100b=（80a+100b）×22%，化简得60a+80b=62.4a+78b，因此a:b=5:6

例2：（2016联考）某高校艺术学院分音乐系和美术系两个系别，已知学院男生人数占人数的 30％，且音乐系男女生人数之比为 1：3，美术系男女生人数之比为 2：3，问音乐系和美术系的总人数之比为多少？

1. A.5：2
2. B.5：1
3. C.3：1
4. D.2：1

解析

6. 音乐系男生人数占比=音乐系男生/音乐系总人数，美术系男生人数占比=美术系男生/美术系总人数，因为音乐系男女人数之比为 1：3，可得音乐系男生人数占比为1/4=25%，美术系男女人数之比为 2：3 可得美术系男生人数占比2/5=40%，混合后男生人数占人数的 30%，A，B 的混合题型，因此采用十字交叉法如下：
   
   显然音乐系和美术系男生人数之比为 2：1，故本题选 D

例3：（2019江苏）某银行为一家小微企业提供了年利率分别为6％、7％的甲、乙两种贷款，期限均为一年。若两种货款的合计数额为400万元，企业需付利息总额为25万元，则乙种贷款的数额是：

1. A.100万元
2. B.120万元
3. C.130万元
4. D.150万元

解析

6. 甲乙年利率分别为6％、7％，两种货款的合计数额为400万元，企业需付利息总额为25万元，则两种合计年利率为$\frac{25}{400}$=6.25%，使用十字交叉，甲：乙=（7%-6.25%）:（6.25%-6%）=3：1 ，总共400万，乙占一份，则乙为100万元，所以答案为A

例4：（2016北京）将1千克浓度为X的酒精，与2千克浓度为20%的酒精混合后，浓度变为0.6X。则X的值为？

1. A.50%   B.48
2. C.45%   D.40%

解析

3. 典型的溶液混合。
   
   得到$\frac{0.6X-0.2}{0.4X}$=$\frac{1}{2}$。解得X=50%，选A

例5：（2017联考）甲乙两队举行智力抢答比赛，两队平均得分为92分，其中甲队平均得分为88分，乙队平均得分为94分，则甲乙两队人数之和可能是:

1. A.20   B.21
2. C.23   D.25

解析

3. 平均数问题，甲队平均分=$\frac{\mathrm{甲}\mathrm{队}\mathrm{总}\mathrm{分}}{\mathrm{甲}\mathrm{队}\mathrm{人}\mathrm{数}}$，乙队平均分=$\frac{\mathrm{乙}\mathrm{队}\mathrm{总}\mathrm{分}}{\mathrm{乙}\mathrm{队}\mathrm{人}\mathrm{数}}$，混合后两队平均分=$\frac{\mathrm{两}\mathrm{队}\mathrm{总}\mathrm{分}}{\mathrm{两}\mathrm{队}\mathrm{人}\mathrm{数}}$，因此采用十字交叉法，可得甲乙两队人数比=（94-92）：（92-88）= 2：4 = 1：2，那么甲：乙=1：2，则甲乙总人数为3的倍数，选B。